Die Winkelfunktionen

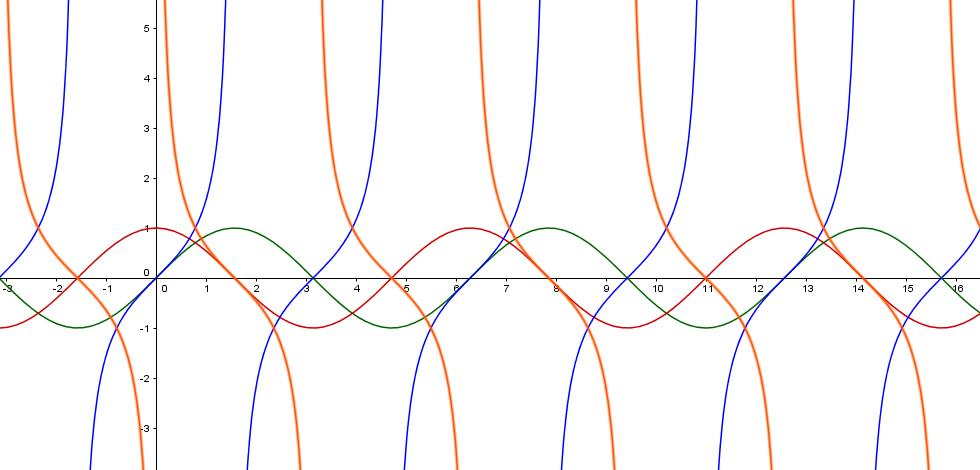
Beziehungen zwischen Winkelfunktionen

sin(x)=sqrt[1-cos(x)²]

cos(x)=sqrt[1-sin(x)²]

tan(x)=sin(x)/cos(x)

cot(x)=cos(x)/sin(x)=1/tan(x)

Reihendarstellungen

sin(x)=x-x³/3!+x⁵/5!-x⁷/7!+x⁹/9!-x¹¹/11!+x¹³/13!-x¹⁵/15!+x¹⁷/17!...

cos(x)=1-x²/2!+x⁴/4!-x⁶/6!+x⁸/8!-x¹⁰/10!+x¹²/12!-x¹⁴/14!+x¹⁶/16!+x¹⁸/18!...

Beachte: Der Winkel (hier x) muss in Radiant angegeben sein! x^rad=pi*x°/180

Da die Reihendarstellungen des Tangens (=tan) und Kotangens (oder auch "Cotangens" =cot) etwas komplizierter sind, werden sie hier nicht beschrieben!
Diese Funktionen können jedoch, wie in den Beziehungen zwischen Winkelfunktionen beschrieben, berechnet werden.

Kettenbrüche

sin(x)=x/(1+x²/(2*3-x²+2*3*x²/(4*5-x²+4*5*x²/(6*7-x²+6*7*x²/(…)))))

Die Funktionen cos, tan und cot können, wie in den Beziehungen zwischen Winkelfunktionen beschrieben, berechnet werden.

Die Umkehrungsfunktionen

Beziehungen

Reihendarstellungen

arcsin(x)=x+1/2*x³/3+(1*3)/(2*4)*x⁵/5+(1*3*5)/(2*4*6)*x⁷/7+(1*3*5*7)/(2*4*6*8)*x⁹/9+...

arccos(x)=pi/2-x-1/2*x³/3-(1*3)/(2*4)*x⁵/5-(1*3*5)/(2*4*6)*x⁷/7-(1*3*5*7)/(2*4*6*8)*x⁹/9-...

arctan(x)=x-x³/3+x⁵/5-x⁷/7+x⁹/9-x¹¹/11+x¹³/13-x¹⁵/15+x¹⁷/17-x¹⁹/19+x²¹/21-...

arccot(x)=pi/2+x+x³/3-x⁵/5+x7/7-x⁹/9+x¹¹/11-x¹³/13+x¹⁵/15-x¹⁷/17+x¹⁹/19-x²¹/21+...

Kettenbrüche

arcsin(x)=x*sqrt(1-x²)/(1-2*x²/(3-2*x²/(5-3*4*x²/(7-3*4*x²/(9-5*6*x²/(…))))))

arctan(x)=x/(1+x²/(3+2²*x²/(5+3²*x²/(7+4²*x²/(9+5²*x²/(11+6²*x²/(…)))))))

Die Funktionen arccos und arccot können, wie in den Beziehungen beschrieben, berechnet werden.